In der Mathematik rechnen wir mit Zahlen. Man unterscheidet verschiedene Zahlenarten (Klassen). Die wichtigsten Zahlenarten sind:
- Natürliche Zahlen
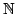
- Ganze Zahlen
- Negative Zahlen
- Rationale Zahlen
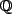
- Irrationale Zahlen
- Reelle Zahlen
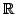
- Komplexe Zahlen
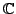
zu Natürliche Zahlen
Natürliche Zahlen sind die Zahlen 1,2,3,4,5,6,7,8, ..., also diejenigen, die jeder zum Zählen braucht.Prinzipiell gilt daher: Alles was ich abzählen kann, wird als natürlich Zahl bezeichnet.
Wie man sieht, fehlt in der obigen Aufzählung die „0“. Manche Mathematiker rechnen die „0“ dazu, andere aber nicht.
Die Menge der natürlichen Zahlen wird mit dem Formelzeichen
abgekürzt.Sie umfasst entweder die positiven ganzen Zahlen
oder die nichtnegativen ganzen Zahlen
Die natürlichen Zahlen bilden mit der Addition und der Multiplikation zusammen eine mathematische Struktur. Die natürlichen Zahlen lassen sich noch weiter unterteilen. Es gibt noch die geraden Zahlen, die ungeraden Zahlen und die Primzahlen.
Als gerade Zahlen werden alle Zahlen bezeichnet, die sich durch 2 ohne Rest teilen lassen. Dies sind die Zahlen 2, 4, 6, 8, 10, 12...
Die ungeraden Zahlen liegen dazwischen: 1, 3, 5, 7, 9, 11....
Die sogenannten Primzahlen hingegen lassen sich nur durch sich selbst und durch 1 ohne Rest teilen. Die ersten Primzahlen lauten: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29...
Darüber hinaus gibt es noch die Begriffe „Kardinalzahl“ und „Ordnungszahl“, die im Moment noch nicht so wichtig für uns sind. Wer´s genauer wissen will, bitte googeln.
zu Ganze Zahlen
Als ganze Zahl bezeichnet man alle Zahlen, die die nur Nullen hinter dem Komma aufweisen. Beispiele: …. -4, -3, -2, -1, 0, 1, 2, 3, 4...
Die Menge
heißt Menge der ganzen Zahlen.
Die ganzen Zahlen enthalten also alle natürlichen Zahlen einschl. der Null und alle diese Zahlen mit einem Minuszeichen davor. Die Menge der ganzen Zahlen ist total geordnet, in der Reihenfolge
d. h. man kann je zwei ganze Zahlen vergleichen. Man spricht von positiven
, nichtnegativen 
, negativen 
und nichtpositiven 
ganzen Zahlen. Die Zahl 0 selbst ist weder positiv noch negativ.
Diese Ordnung ist verträglich mit den Rechenoperationen, d. h.
ist
und 
, dann ist 
,ist
und 
, dann ist 
.Wie die Menge der natürlichen Zahlen ist auch die Menge der ganzen Zahlen abzählbar.
zu Negative Zahlen
Die negativen Zahlen entstehen wenn man von einer Zahl eine größere subtrahiert.
Alle Zahlen bestehen aus zwei Teilen, dem Betrag und dem Vorzeichen.
Anmerkung:
Der Betrag sind die "normalen" Zahlen. Wenn man bei einer Zahl vom Betrag spricht, setzt man die Zahl zwischen 2 Striche, z.B. I2I bedeutet „Betrag von 2“
Das Vorzeichen ist entweder + (Plus, und wird normalerweise nicht mitgeschrieben) oder - (Minus).
Negative Zahlen sind z.B. -1, -2, -3, -4, ....... usw.
Anmerkung: Hier Aufpassen!!
Beispiel: Was ist 10 - 35?
Da 35 größer als 10 ist, geht das eigentlich nicht. Daher drehen wir die Zahlen zunächst um:
Das heißt wir berechnen 35 -10, das ergibt 25 und das nennen wir „Betrag“.
Vor diesen Betrag schreiben wir jetzt das Vorzeichen: -25 ist somit das Endergebnis von von 10 - 35:
zu Rationale Zahlen
Jede rationale Zahl ist eine reelle Zahl, die als Verhältnis zweier ganzer Zahlen dargestellt werden kann. Man spricht auch von „gebrochener Zahl“. Die Menge aller rationalen Zahlen wird mit dem Formelzeichen
(von „Quotient“) bezeichnet. Die Menge
heißt Menge der rationalen Zahlen.Sie umfasst alle Zahlen, die sich als Bruch darstellen lassen, der sowohl im Zähler als auch im Nenner ganze Zahlen enthält.
Im Nenner darf aber nie eine „0“ stehen. Die Division durch Null ist für uns nicht zulässig.
Zum Beispiel sind rationale Zahlen: 1/2, 1/3, 4/6, 167/ 346 ... usw.
zu Irrationale Zahlen
Rationale Zahlen kann man als Bruch darstellen, irrationale Zahlen können jedoch nicht durch einen ganzzahligen Bruch dargestellt werden!
Daher kann man definieren:
Irrationalen Zahlen sind alle Kommazahlen, die nicht als Bruch dargestellt werden können. Dies sind meistens Zahlen, die durch unendliche Folgen und Reihen zustande kommen (so wie zum Beispiel die Zahl Pi).
Zieht man zum Beispiel die Wurzel aus der Zahl 2, erhält man etwa die Zahl 1,4142. Diese Zahl ist jedoch ungenau, denn es folgen bei der Wurzel aus 2 unendlich viele Stellen nach dem Komma. Dies gilt auch für die Kreiszahl π ( gesprochen: pi ), bei der in der Schule meist der Wert 3,14 als Näherung verwendet wird. In der Praxis bricht man also nach einer bestimmten Stelle nach dem Komma ab und erhält somit eine endliche Dezimalzahl ( Kommazahl ).
zu Reelle Zahlen
Fasst man alle rationalen und irrationalen Zahlen zu einer Menge zusammen, erhält man die sogenannten reellen Zahlen.
Die Menge der reellen Zahlen entspricht der Menge aller Punkte der Zahlengeraden. Zu ihrer Bezeichnung wird das Symbol
verwendet.Die reellen Zahlen werden unterschieden in:
a) rationale Zahlen
b) ganze Zahlen
c) natürliche Zahlen
= 
oder 
= 
d) irrationale Zahlen
= die Menge aller Elemente von 
, die nicht in 
liegen. Diese lassen sich wiederum unterteilen in:irrationale algebraische Zahlen und transzendente Zahlen.
zu Komplexe Zahlen
Das Rechnen mit komplexen Zahlen erfolgt erst an den Fachhochschulen bzw. Technischen Universitäten, vorzugsweise wenn du Dipl.Ing. für Elektrotechnik werden willst.
Die komplexen Zahlen erweitern den Zahlenbereich der reellen Zahlen derart, dass die Gleichung
lösbar wird.Dies gelingt durch Einführung einer neuen Zahl
mit der Eigenschaft 
. Diese Zahl 
wird als imaginäre Einheit bezeichnet. In der Technik wird stattdessen der Buchstabe 
verwendet, um einer Verwechslung mit einer (durch 
bezeichneten) von der Zeit 
abhängigen Stromstärke vorzubeugen.