Du erinnerst dich, die Geradengleichung können wir allgemein beschreiben mit der Formel:
Auch für die quadratische Gleichung, also für eine Funktion 2.Ordnung, gibt es eine allgemeine Formel, nämlich:
In dieser Formel sind a, b, und c irgendwelche Zahlen, wobei a nicht Null sein darf, da wir sonst ja keine quadratische Gleichung mehr haben!
Beispiel: wenn a=1, b= 8 und c=2 ist, lautet die quadratische Gleichung:
_________________________________________________________________
Wie löse ich quadratische Gleichungen?
Es gibt drei Verfahren zum Lösen quadratischer Gleichungen:
- die p-q-Formel
- die Mitternachtsformel bzw. die abc-Formel
- der Satz von Vieta
1. die p-q-Formel
Üblicherweise löst man quadratische Gleichungen mit der sogenannten p-q-Formel.
Dazu bringt man jede quadratische Gleichung auf die Form:
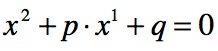
Danach verwenden wir die p-q-Formel:
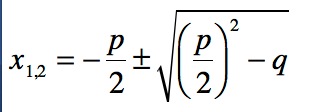
Die Formel sieht schlimmer aus als es in Wirklichkeit ist. Wir rechnen jetzt anhand dieser Formel die Beispielgleichung
aus:
a war 1, p = 8 und q = 2. Setzen wir diese Werte in die p-q-Formel ein, erhalten wir:
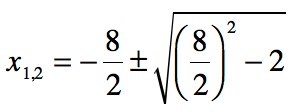
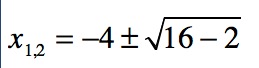
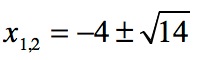
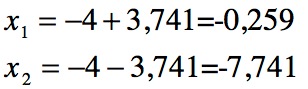
Die beiden Nullstellen lauten nun:
N1 (-0,259 / 0) und N2 (-7,741 / 0).
In diesem Beispiel hat die quadratische Gleichung 2 Lösungen . Das ist aber nicht immer so. Möglich wären auch nur eine Lösung oder gar keine Lösung.
Die quadratische Gleichung ist nämlich zeichnerisch darstellbar als eine Parabel.
Logischerweise kann die Parabel - wie in diesem Beispiel- die x-Achse zweimal schneiden. Daher haben wir dann auch zwei x-Werte x1 und x2. Die Parabel kann die x-Achse aber auch nur berühren. Dann gibt es genau einen x-Wert. Als dritte Möglichkeit kommt in Frage, dass die Parabel die x-Achse weder berührt noch schneidet.Dann gibt es keinen x-Wert.
Wie sieht nun in unserem Beispiel die Parabel aus?
Zum Konstruieren der Parabel machen wir für
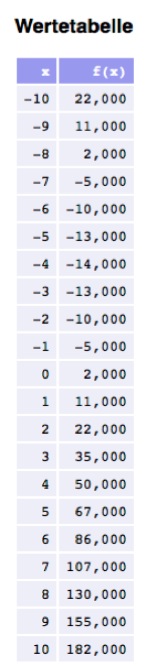
Tragen wir diese Werte in ein Koordinatensystem ein, erhalten wir folgende Parabel:
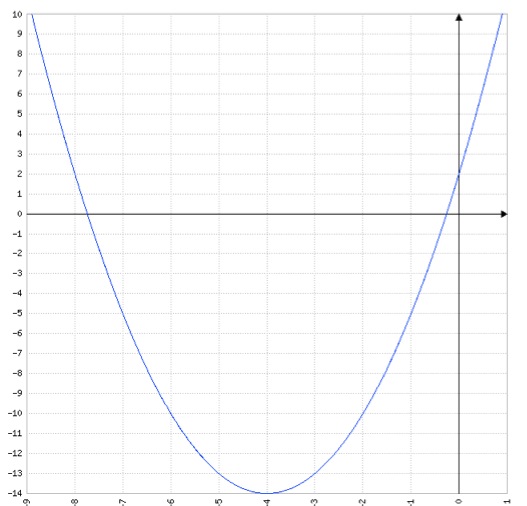
Nach diesem exemplarischen Beispiel, üben wir das Gleich noch einmal mit anderen Zahlen. Gegeben ist eine Funktionsgleichung 2. Ordnung (= quadratische Gleichung), die sich folgendermassen beschreiben lässt:
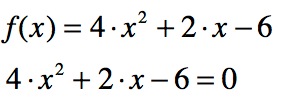
in diesem Fallbeispiel ist a = 4, b = 2 und c = -6
Zum Anwenden der p-q-Formel musst du nun zuerst herausfinden, was p und q ist.
Am Anfang muss immer
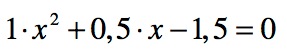
Du siehst nun, dass p = 0,5 und q = -1,5 ist.
Wenn du nun die p-q-Formel anwendest, ergibt sich:
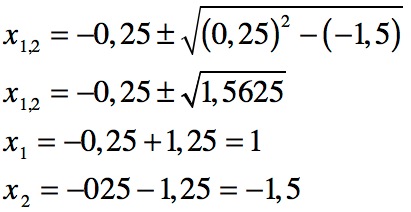
Die beiden Nullstellen dieser Funktionsgleichung 2.Grades heissen daher:
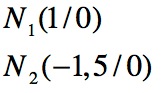
Auch für diese Gleichung erstellen wir eine Wertetabelle und zeichnen den Graphen:
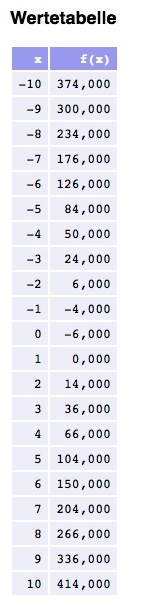
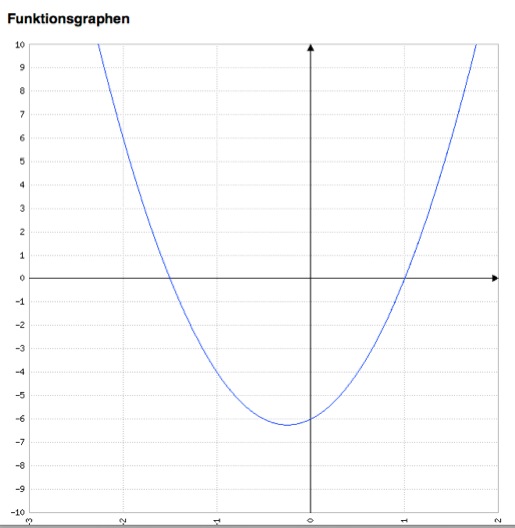
2. die Mitternachtsformel (abc-Formel)
Die allgemeine Form der quadratischen Gleichung ist:
Die Normalform ist:
Daraus lässt sich durch entsprechende Umformungen die folgende „Mitternachtsformel“ als Lösung für die quadratische Gleichung herleiten:
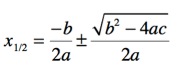
Der Wurzelausdruck heißt in der Fachsprache „Diskriminante D“.
Für die Diskriminante D gibt es drei Möglichkeiten:
- 1. D > 0 : es gibt es zwei verschiedene reelle Lösungen
- 2. D = 0 : es gibt es eine reelle Lösung
- 3. D < 0 : es gibt keine reelle Lösung
Beispiel:
wir lesen ab: a= 2, b = -4 und c = -16
wir setzen diese Werte in die Mitternachtsformel ein und erhalten dann:
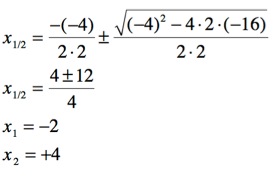
Die beiden Nullstellen dieser Funktionsgleichung 2.Grades heissen daher:
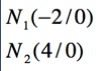
Auch für diese Gleichung erstellen wir eine Wertetabelle und zeichnen den Graphen:
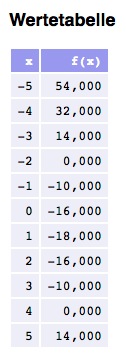
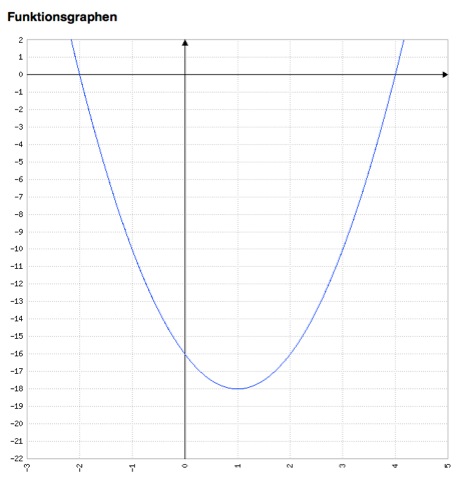
3. der Satz von Vieta
Der französische Mathematiker F.Vieta (1560 - 1603) fand heraus, dass zwischen p und q und x1 und x2 folgender Zusammenhang besteht:
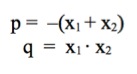
Wir nehmen als Beispiel nochmals die obige Gleichung:
Teilen wir durch 2 erhalten wir:
p = -2 und q = -8
Gemäß dem Satz von Vita müssen wir nun zwei Zahlen finden
a) deren Summe -2 ist und
b) deren Produkt 8 ist.
Da es unendlich viele Möglichkeiten gibt, die Summe -2 zu bilden, konzentrieren wir uns auf die Produktbildung von 8.
Hierfür benötigen wir alle Faktoren von -8. Diese sind z.B.
- 2 x -4
- 1 x -8
- 4 x -2
Nun müssen zwei Faktoren finden, deren Summen -2 ergibt. Dafür kommen nur 2 und -4 in Frage!
Die Nullstellen der Gleichung wären damit:
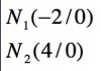
_________________________________________________________________
Linearfaktorenzerlegung:
Mit den Lösungen können wir das Polynom (die Funktionsgleichung 2.Grades)
Daher eignet sich der Satz von Vieta auch , um quadratische Polynome zu faktorisieren. Unsere obige Gleichung lässt sich dann folgendermaßen darstellen:
_________________________________________________________________
Anmerkung zur Normalparabel
Die vorigen Beispiele zeigen als Graph die typische Form einer Parabel. Von einer Normalparabel sprechen wir, wenn folgende Bedingungen erfüllt sind:
- Die Normalparabel wird definiert durch die Funktionsgleichung
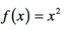
- Die Definitionsmenge ist die Menge aller x-Werte, welche die Funktionswerte annehmen kann.
- Die Wertemenge ist die Menge aller y-Werte, die der Graph annehmen kann. Im Falle der Normalparabel sind nur positive y-Werte möglich.
- Der tiefste Punkt der Normalparabel, der sogenannte Scheitelpunkt S ist S (0/0). Hier nimmt die Funktion f ihren kleinsten Funktionswert an.
- Die Normalparabel ist nach oben geöffnet.
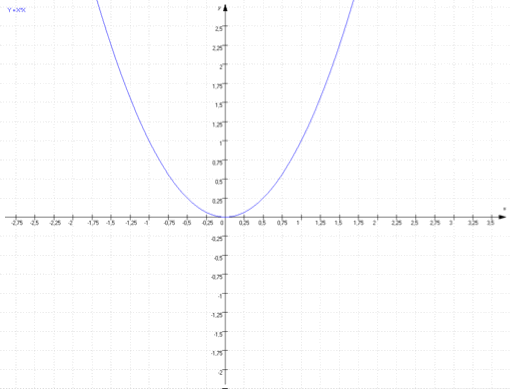
Nun kann man - ausgehend von dieser Normalparabel- die Parabel nach rechts oder nach links, nach oben oder nach unten usw. verschieben. Das Bild bzw. der Graph ändert sich entsprechend und damit auch die Formel.
Beispiel 1:
Verschieben der Normalparabel nach rechts
Bei der Ausgangsparabel mit der Gleichung
Verschieben wir die Normalparabel um die Strecke d in Richtung der x-Achse wird aus
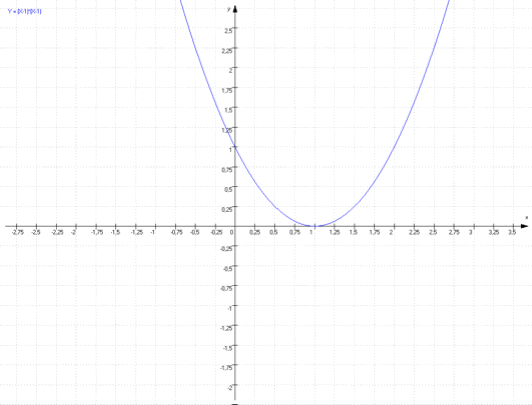
Im obigen Beispiel siehst du, dass der Scheitelpunkt der verschobenen Parabel auf S (1/0) liegt. Daher lautet die dazugehörende Gleichung in diesem Fall:
Beispiel 2:
Verschieben der Normalparabel nach links
Wie du dir schon denken kannst, verschiebt sich die Normalparabel nach links, wenn in der Klammer aus dem Minus-Zeichen ein Plus-Zeichen wird.
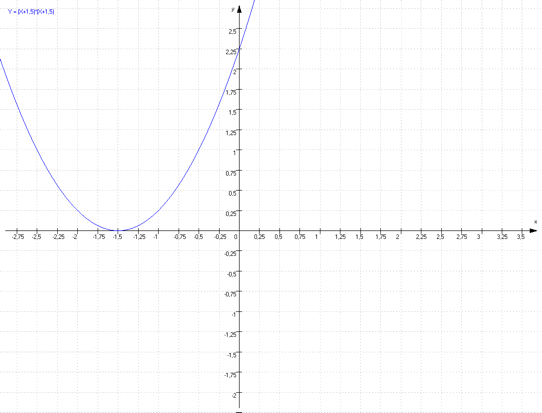
Im obigen Beispiel siehst du, dass der Scheitelpunkt der verschobenen Parabel auf S (-1,5/0) liegt. Daher lautet die dazugehörende Gleichung in diesem Fall:
Zusammenfassung:

Beispiel 3:
Verschieben der Normalparabel nach oben
Genauso wie wir die Normalparabel nach rechts und links verschieben können, kannst du natürlich auch die Parabel nach oben und unten verschieben.
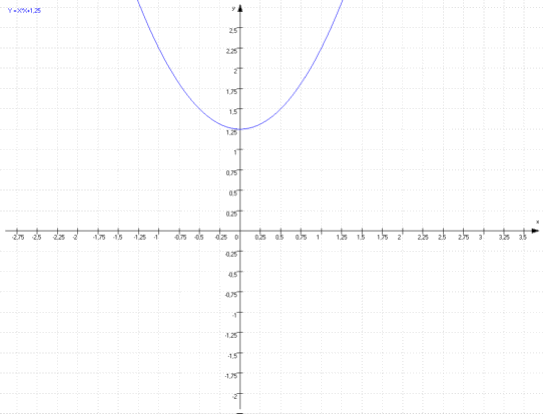
In diesem Beispiel habe ich die Normalparabel um die Strecke c = 1,25 mach oben verschoben. Der Scheitelpunkt der Parabel liegt bei S (0/1,25).
Die dazugehörende Parabelgleichung heißt nun:
Beispiel 4:
Verschieben der Normalparabel nach unten
Wie du dir auch hier schon denken kannst, verschiebt sich die Normalparabel nach unten, wenn aus dem „+c“ ein „-c“ wird.
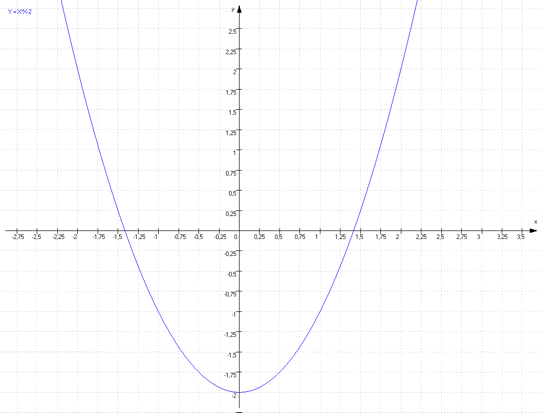
Der Scheitelpunkt diese Parabel liegt bei S (0/-2).
Die dazugehörende Parabelgleichung heißt nun:
Zusammenfassung:

Aufgabe 1
Bestimme die Parabelgleichung für den folgenden Graphen:
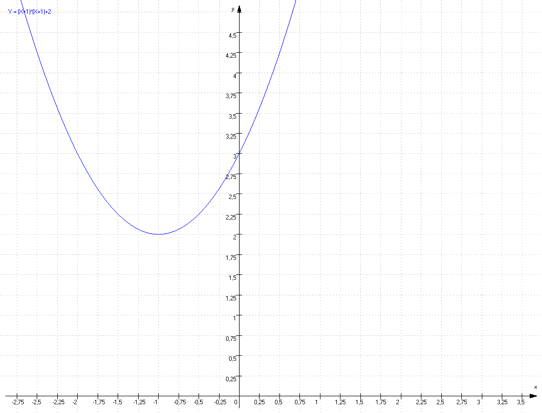
Zunächst stellst du fest, wo der Scheitelpunkt dieser Parabel liegt!
Antwort: Der Scheitelpunkt S heißt S (-1/ +2)
Nun wenden wir das vorher Gelernte -Verschiebung nach links und zusätzlich Verschiebung nach oben- hier an und kommen auf folgende Gleichung:
Aufgabe 2
Bestimme die Parabelgleichung für den folgenden Graphen:
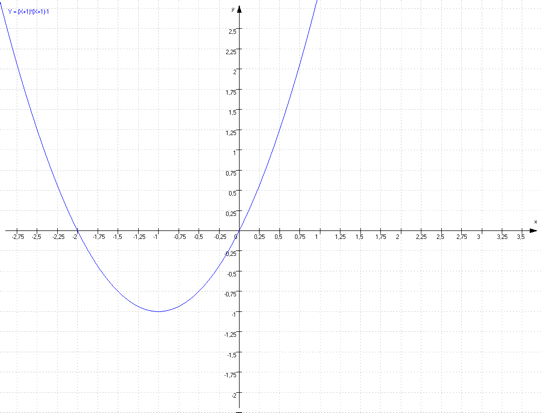
Zunächst stellst du auch hier fest, wo der Scheitelpunkt dieser Parabel liegt!
Antwort: Der Scheitelpunkt S heißt S (-1/ -1)
Nun wenden wir das vorher Gelernte -Verschiebung nach links und zusätzlich Verschiebung nach unten- hier an und kommen auf folgende Gleichung:
Aufgabe 3
Achtung! Wir können auch umgekehrt blitzschnell eine Parabel zeichnen, wenn wir bei einer vorgegeben Funktionsgleichung die Linearfaktorenzerlegung anwenden und den Scheitelpunkt dann ablesen können. Wie das geht, üben wir am folgenden Beispiel:
Gegeben ist die folgende Funktionsgleichung:
Zum Umformen der Gleichung erinnern wir uns an den Satz von Vieta
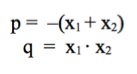
und wenden folgenden Trick an: die 11 stört uns, da wir kein Produkt finden, das eine 11 ergibt. Also arbeiten wir mit der 9 und denken 11 = 9 +2. Welche beide Zahlen ergeben als Summe die 6 und als Produkt die 9?
Da kommt nur die 3 und die 3 in Frage: 3 +3= 6 und 3 mal 3 = 9
Daher lautet die Gleichung in Linearfaktoren zerlegt nun:
- Jetzt können wir den Scheitelpunkt der Parabel direkt aus der Gleichung wieder ablesen: S (+3/+2).
Der Funktionsgraph sieht dann folgendermaßen aus:
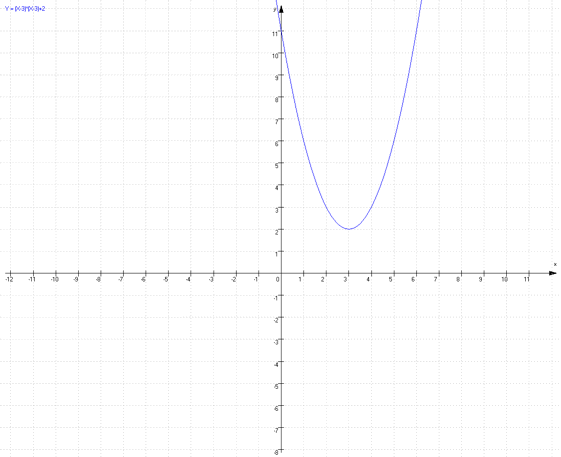
Stauchen und Strecken der Normalparabel
Die allgemeine Formel für die Normalparabel ist
wobei a = 1 ist.
Für den Fall, dass a >1 oder a <1 ist, wird die Parabelform entsprechend gestreckt oder gestaucht.
Fall 1: a >1
Der Normalparabel ist wegen a = 4 entsprechend „gestaucht“ und sieht so aus:
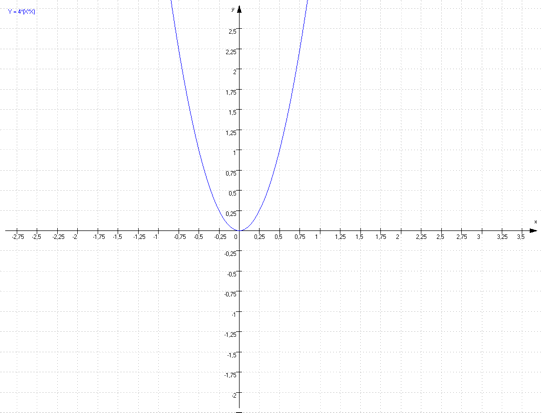
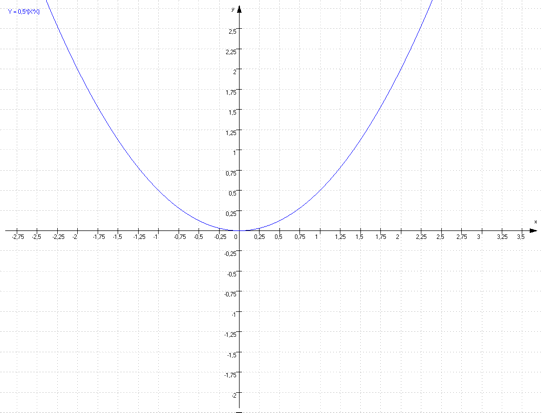
Fall 2: a <1
Der Normalparabel ist wegen a = 0,5 entsprechend „gestreckt“ und sieht so aus:
AUFGABE
Gegeben ist die Funktionsgleichung
Zeichne den Funktionsgraphen!
Zunächst bestimmen wir den Scheitelpunkt S. Wir lesen ab und erhalten S (0/-4).
Nun stellen wir eine kleine Wertetabelle auf:
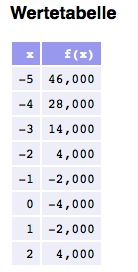
Jetzt haben wir genügend Informationen um den Graph zu zeichnen:
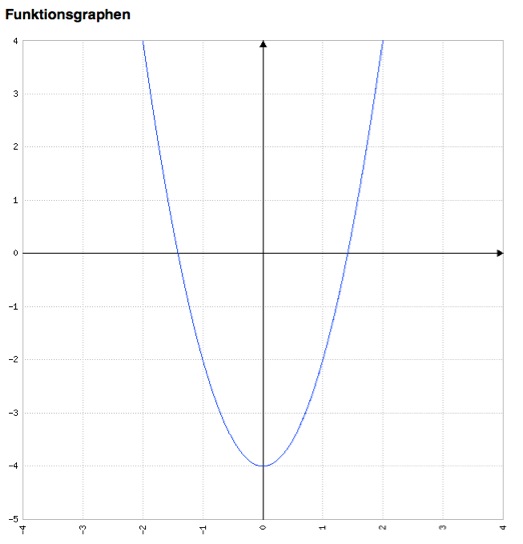
_________________________________________________________________
Aufstellen einer Funktionsgleichung 2.Grades mit Hilfe von drei gegebenen Punkten
Du erinnerst dich: Zum Aufstellen einer Geradengleichung (Funktionsgleichung 1.Grades) benötigt man zwei Punkte.
Willst du eine Parabelgleichung aufstellen sind 3 Punkte notwendig.
Die allgemeine Form der quadratischen Gleichung lautet:
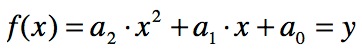
In dieser Gleichung finden wir drei Unbekannte: nämlich a, b und c. Daher benötigen wir drei voneinander unabhängige Gleichungen. Erst mit diesem Gleichungssystem können wir die Aufgabe lösen.
Beispiel:
Gegeben sind die Punkte P1 (1/2), P2 (5/4) und P3 (3/-1).
Indem wir die entsprechenden x- und y-Werte der drei Punkte verwenden, stellen wir folgendes Gleichungssystem auf:

Um die Koeffizienten a2, a1 und ao zu bestimmen, müssen wir verschiedene Additions- bzw. Substitutionsverfahren anwenden.
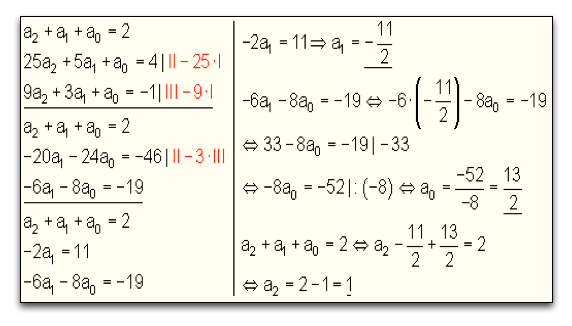
Die gesuchte Funktionsgleichung die durch die drei Punkte P1 (1/2), P2 (5/4) und P3 (3/-1) geht, heißt:
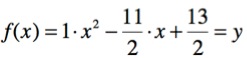
_________________________________________________________________