Im folgenden einfachen Beispiel ist eine Gerade vorgegeben.
Typische für eine Gerade ist, dass man mit Hilfe von zwei Punkten die Gerade zeichnen und bestimmen kann.
Beispiel 1:
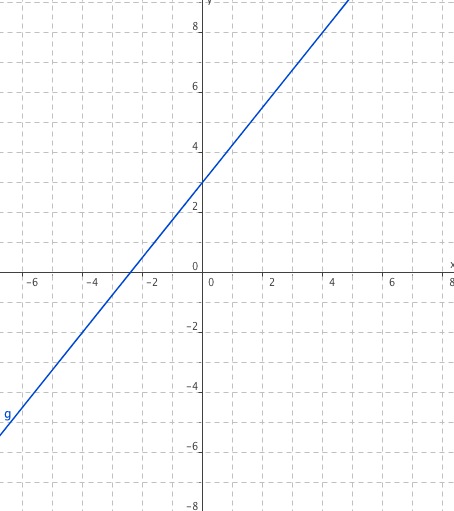
Wenn du den „Graph“ (so sagt man dazu) genau betrachtest, dann siehst du, dass
1. die Gerade an der Stelle X = -2,5 die Abszisse (das ist die waagerechte x-Achse) schneidet. Der Schnittpunkt an dieser Stelle heißt dann (-2,4/0).
2. die Y- Achse, also die Ordinate, wird von der Geraden an der Stelle y = 3 geschnitten. Dieser Schnittpunkt heißt dann (0/3)
Nun kann man mit diesen beiden Punkten (-2,4/0) und (0/3) die Geradengleichung „aufstellen“.
Die allgemeine Geradengleichung heißt: y = mx + b
Darin ist m die Steigerung der Gerade und b der sogenannte Achsenabschnitt.
Deine Aufgabe besteht nun darin, heraus zu finden, was „m „ und „b“ ist.
Wie du schon gelernt hast, benötigt man zum Lösungen einer Gleichung mit 2 Unbekannten (hier: m und b)
ein Gleichungssystem mit 2 unabhängigen Gleichungen.
Durch die Vorgabe der beiden Punkte (-2,4/0) und (0/3) haben wir diese beiden Gleichungen. Wir setzen jeweils „x“ und „y“ ein und erhalten:
0 = -2,4m + b
3 = 0m + b
Daraus folgt: b = 3
Setzen wir nun b = 3 in die erste Gleichung ein, erhalten wir:
0 = -2,4m +3 --> 2,4m = 3 ---> m = 3/2,4 ---> m = 6/4 = 1,25
Die gesuchte Gleichung heißt nun: y = 1,25x + 3
Probe:
Zur Probe setzt du nun eine beliebigen x-Wert ein und schaust in der Zeichnung nach, ob es stimmt:
Zum Beispiel setzen wir x = - 4 in die Gleichung ein und erhalten dann:
y = (- 4) *(+ 1,25) + 3 = -5 + 3 = -2
Schau in der Zeichnung oben nach, ob es stimmt!
_______________________________________________________________________________________________
Beispiel 2:
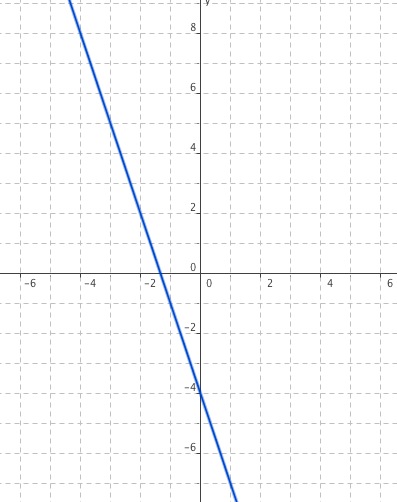
Zum Aufstellen der Geradengleichung brauchst du 2 Punkte von dieser Geraden. Wir machen es und einfach und suchen 2 Stellen, wo wir bequem ablesen können, z.B.
Punkt 1 : (0/-4)
Punkt 2: (-3/5)
Die allgemeine Form der Geradengleichung heißt:
y = mx + b
Die beiden vorhandenen Gleichungen lauten:
- 4 = 0m + b
+5 = -3m + b
daraus folgt: b = - 4
und b = -4 in die obige Gleichung eingesetzt, ergibt 3 m = - - 5 - 4 = - 9
Also ist m = -3
Somit lautet die Geradengleichung für das obige Beispiel:
y = - 3*x - 4
Wir machen wieder die Probe!
Probe:
Zur Probe setzt du nun eine beliebigen x-Wert ein und schaust in der Zeichnung nach, ob es stimmt:
Zum Beispiel setzen wir x = - 2 in die Gleichung ein und erhalten dann:
y = (- 2) *(- 3) - 4 = + 6 - 4 = + 2
Schau in der Zeichnung oben nach, ob es stimmt!
________________________________________________________________________________________________
Beispiel 3:
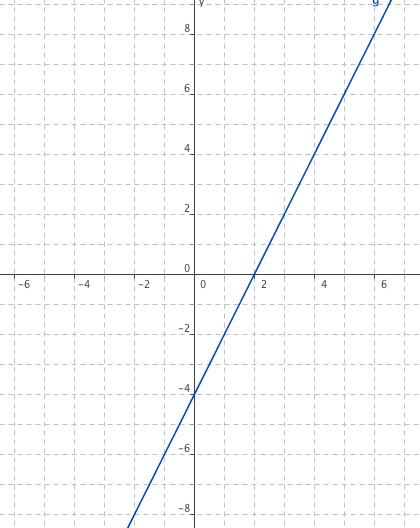
Zum Aufstellen der Geradengleichung brauchst du 2 beliebige Punkte von dieser Geraden. Wir machen es uns wieder einfach und suchen 2 Stellen, wo wir bequem ablesen können, z.B.
Punkt 1 : (0/-4)
Punkt 2: (4/ 4)
Die allgemeine Form der Geradengleichung heißt:
y = mx + b
Die beiden vorhandenen Gleichungen lauten:
Gleichung (1): -4 = 0m + b
Gleichung (1): +4 = 4m + b
aus Gleichung (1) folgt: b = - 4
aus Gleichung (2) folgt: + 4 = 4m -4
daher ist 4m = 8 ---> m = 2
Wenn m = 2 ist und b = -4, lautet die Geradengleichung
y = 2x -4
Wir machen wieder die Probe!
Probe:
Zur Probe setzt du nun eine beliebigen x-Wert ein und schaust in der Zeichnung nach, ob es stimmt:
Zum Beispiel setzen wir x = + 6 in die Gleichung ein und erhalten dann:
y = ( 2) *( 6) - 4 = 12 - 4 = + 8
Schau in der Zeichnung oben nach, ob es stimmt!________________________________________________________________________________________________
Nun wollen wir einmal den Schnittpunkt von 2 Geraden bestimmen:
Im folgenden Beispiel siehst du 2 Geraden. Überlege nun wie du es schaffst, den „Schnittpunkt S“ der beiden Geraden zu bestimmen?
Dafür brauchst du eine Gleichung für die Gerade a und für die Gerade b.
Heute verrate ich dir diese Gleichung.
Nächste Woche musst die Gleichung aus der Zeichnung erkennen können!!!
Gleichung für die Gerade a: y= x +2
Gleichung für die Gerade b: y= -x+1
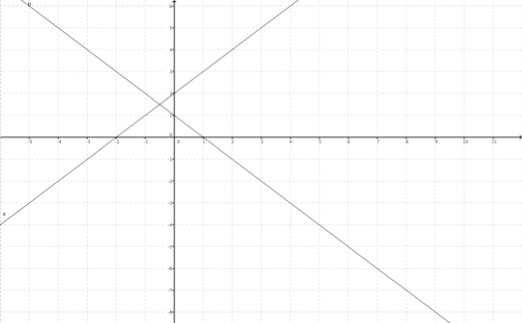
Nun zur Lösung:
Die gerade a und die Gerade b treffen sich am Punkt „S“. Das heißt also, an dieser Stelle haben die beiden Geraden dasselbe „x“ und dasselbe „y“. Daher können wir die beiden Gleichungen gleichsetzen.
Wir schreiben nun:
x + 2 = -x +1
... nach „Hühner zu Hühner und Eier zu Eier“ erhalten wir
2x = -1, darauf folgt: x = -0,5
Setzen wir nun x = -0,5 in eine der beiden Gleichungen ein, erhalten wir für y:
y = -0,5 + 2 = 1,5 oder y = - (-0,5) + 1 = 1,5
Antwortsatz: Der Schnittpunkt der beiden Geraden liegt bei S (-0,5/1,5).
Und jetzt kommt noch ein einfaches Beispiel zum wiederholen:
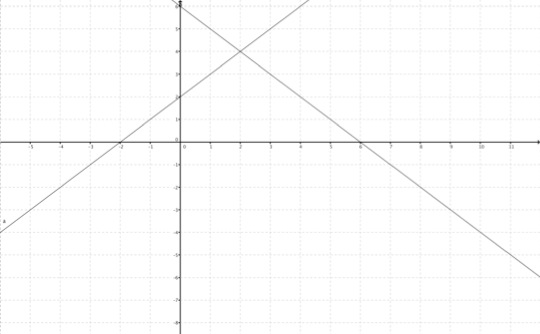
Gerade a: y = x + 2
Gerade b: y = -x +6
Berechne den Schnittpunkt S, indem du die beiden Geradengleichungen gleich setzst.
x + 2 = - x + 6
2x = 4 daraus folgt x = 2
Als y ergibt sich dann: y = 2 + 2 = 4
Der gesuchte Schnittpunkt S lautet daher: S(2/4)
________________________________________________________________________________________________
....und noch ein Beispiel (denn „Übung macht den Meister“!)
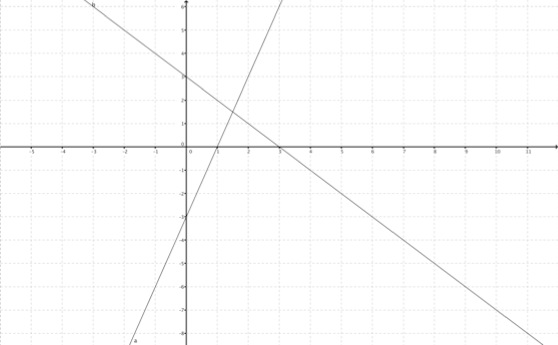
Gerade a; y = 3x - 3
Gerade b: y = -x +3
Berechne den Schnittpunkt S, indem du die beiden Geradengleichungen gleich setzst.
3x - 3 = -x + 3
4x = 6 und darauf ergibt sich für x: x= 1,33333333......
Als y ergibt sich dann: y = 3x 6/4 = 18/4 - 3 = 4,5 - 3 = 1,5
Der gesuchte Schnittpunkt S lautet daher: S(1,33/1,5)
________________________________________________________________________________________________
Nach den drei Beispielen sollst du nun das folgende Beispiel alleine rechnen:
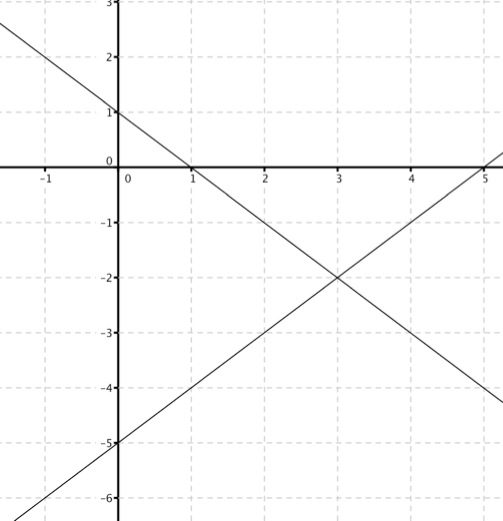
Die Aufgabe lautet also:
Berechne den Schnittpunkt S der beiden Geraden, die durch folgende Geradengleichungen gegeben sind:
a: y = x - 5
B: y = -x + 1
__________________________________________________________________________________________________
Aufstellen einer Geradengleichung
Die allgemeine Form einer Geradengleichung kennst du nun!
Nämlich:
y = mx + b
Das „b“ ist bekanntlich der sogenannte Achsenabschnitt (= der y-Wert des Schnittpunktes der Geraden an der Y-Achse).
Jetzt möchte ich DIR noch erklären, dass man zu „m“ auch „Steigungsfaktor der Geraden“ oder einfach „Steigung“ sagt!
Wichtig:
Jede Gerade ist durch ein Steigungsdreieck gekennzeichnet!
In der folgenden Zeichnung ist das Steigungsdreieck angegeben.:
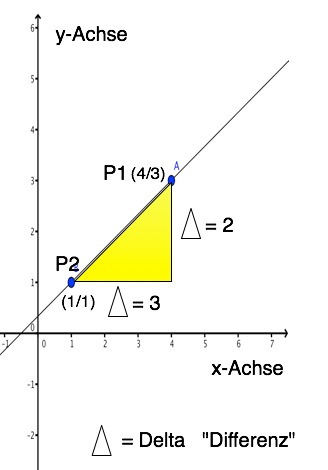
Der Punkt P1 ist gekennzeichnet durch x1 = 4 und y1 = 3.
Der Punkt P2 ist gekennzeichnet durch x2 = 1 und y2 = 1.
Vom Steigungsdreieck zur Steigung m:
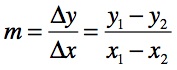
Aus dem Steigungsdreieck kannst du nun leicht ablesen, dass
x1 - x2 = 4 - 1 = 3 und y1 - y2 = 3 - 1 = 2
Wir erhalten dann folgendes Ergebnis für die Steigung m:
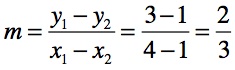
Die Geradengleichung lautet nun:
y = 2/3 x + b
Aber was ist jetzt „b“ (der Achsenabschnitt, wo die Gerade die Y-Achse schneidet!)?
Wir können nun zum Beispiel den Punkt P1 (4/3) in die Gleichung einsetzen. Dann erhalten wir:
3 = (2/3) 4 +b Daraus folgt, dass b = 1/3.
Antwortsatz:
Die Geradengleichung im obigen Beispiel heißt:
y = 2/3 x + 1/3