Die Bruchrechnung brauchen wir, wenn es nicht mehr um „das Ganze“ geht, sondern um Teile eines Ganzen, also um „Bruchstücke“.
Zum Vergleich nehme ich einmal an, ich teile eine Tafel Schokolade -bestehend aus 12 Schokoladenriegel auf drei Personen auf.
Alina bekommt 4 Riegel, Thomas bekommt 3 Riegel und der Rest wird von Reinhard aufgegessen.
Dann haben wir die 12 Riegel folgendermaßen verteilt:
Alina: 4/12 (sprich: vier-zwölftel)
Thomas: 3/12 (sprich: drei-zwölftel)
Reinhard: 5/12 (sprich: fünf-zwölftel)
Alle Bruchstücke zusammen ergeben wieder eine ganze Tafel Schokolade:
und 12/12 kann man „kürzen“, dann haben wir wieder „1“, das heißt eine ganze Schokoladentafel.
Die Zahl über dem Bruchstrich nennen wir „Zähler“ (weil wir haben ja abgezählt, wieviel Schokoladenstücke jeder bekommen hat), die Zahl unter dem Bruchstrich nennen wir „Nenner“.
Wir konnten die Schokoladenteilstücke nur zusammenzählen, weil es Teile von der gleichen Schokolade waren. Wären es Teile einer Birne oder eines Apfels gewesen, wäre das nicht gegangen. Daraus folgt:
Nur gleichnamige Brüche können zusammengezählt („addiert“) oder von einander abgezogen („subtrahiert“) werden.
wichtige Regel:
Zur Addition oder zur Subtraktion von Brüchen, müssen die Brüche zunächst gleichnamig gemacht werden.
Addition von Brüchen
Wenn wir verschiedene Brüche zusammenzählen wollen, geschieht das meistens in drei Schritten:
- Brüche auf einen gemeinsamen Nenner bringen
- Brüche bzw. Zähler von den Brüchen zusammenzählen
- Ergebnisbruch kürzen
Beispiel:
1.Schritt:
gemeinsamer Nenner von 2, 5 und 8. Eine einfache Möglichkeit, den gemeinsamen Nenner zu finden ist 2,5 und 8 malzunehmen („multiplizieren“).
Also rechnen wir: 2 x 5 x 8 = 80
Wenn 80 der gemeinsame Nenner sein soll, rechnen wir 1/2 um in 40/80. In der Mathematik nennt man diesen Schritt „erweitern des Bruches“. Der Bruch hat den gleichen Wert wie zuvor, er wurde nur um „40“ erweitert, damit wir insgesamt eben 1/2 (das sind 1:2) bekommen.
Da „5“ genau 16-mal in „80“ geht, werden durch die Erweiterung aus 1/5 nun 16/80. Die 3/8 erweitern wir zu 30/80.
2.Schritt:
Addition von 40/80 + 16/80 + 30/80.
Die Zähler ergeben zusammen nach Adam Riese und Eva Zwerg: 40 + 16 + 30 = 86
Demnach ergibt sich als Summe der drei Brüche: 40/80 + 16/80 + 30/80 = 86/80
3.Schritt:
Wir kürzen den Gesamtbruch. Kürzen heißt, Zähler und Nenner durch die gleiche Zahl teilen („dividieren“).
Wenn wir mit „2“ kürzen wird aus 86/80 nach der Division der Ergebnisbruch 43/40.
Der gemeinsame Nenner in diesem Beispiel war „80“. Unser Endergebnis könne wir aber auch erreichen, indem wir zunächst das „kleinste gemeinsame Vielfache“ („kgV“) der drei Nenner bestimmen.
Beispiel zur kgV - Bestimmung:
- die Vielfachen von 2 sind: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, .............36, 38, 40, 42, 44, 46, 48 usw.
- die Vielfachen von 5 sind: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60 usw.
- die Vielfachen von 8 sind: 8, 16, 24, 32, 40, 48, 56, 64, usw.
- und das kleinste von diesen Zahlen ist 40
mathematische Schreibweise: kgV (2,5,8) = 40
Mit dem kgV = 40 sieht unsere Addition der Brüche wie folgt aus:
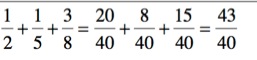
Anmerkung:
Wenn bei den Brüchen die Nenner klein sind, kommt man schnell durch Probieren auf den gemeinsamen Nenner.
Was können wir aber machen, wenn die Nenner groß sind, wie in den folgenden Beispielen:
Beispiel 1:
In diesem Fall müssen wir das kgV (12, 54, 125) suchen.
Eine einfache Möglichkeit das kleinste gemeinsame Vielfache dieser drei Zahlen zu berechnen ist die sogenannte Primfaktorzerlegung.
Primfaktorzerlegung:
Eine Möglichkeit besteht darin, unsere Nenner 12,54,125 in ihre Primfaktoren zu zerlegen. Für das kgV nimmt man dann die Primfaktoren, die in mindestens einer der Zerlegungen vorkommen, und als zugehörigen Exponenten den jeweils größeren der Ausgangsexponenten:
- Primfaktorzerlegung von 12: 2 x 2 x 3 = 2^2 x 3 (Anmerkung: 2^2 sprich: zwei hoch zwei)
- Primfaktorzerlegung von 54: 2 x 3 x 3 x3 = 2 x 3^3
- Primfaktorzerlegung von 125: 5 x 5 x 5 = 5^3
2 x 2 x 3 x 3 x 3 x 5 x 5 x 5 = 13500
Nun können wir unsere drei Brüche gleichnamig machen und nehmen als gemeinsamen Nenner 13500
aus 1/12 wird dann: 1125/13500
aus 24/54 wird dann: 250/13500
aus 5/125 wird dann: 540/13500
Jetzt können wir im nächsten Schritt die gleichnamigen Brüche zusammen zählen:
Wenn wir mit 5 kürzen erhalten wir folgendes Endergebnis:
Diesen Bruch kann man nicht weiter kürzen. Aber man könnte ihn auch als Dezimalzahl schreiben. Die Division von Zähler und Nenner ergibt:
Beispiel 2:
In diesem Fall müssen wir das kgV (125, 1024, 666) suchen.
Eine Möglichkeit besteht darin, unsere Nenner 125, 724, 666 in ihre Primfaktoren zu zerlegen. Für das kgV nimmt man die Primfaktoren, die in mindestens einer der Zerlegungen vorkommen, und als zugehörigen Exponenten den jeweils größeren der Ausgangsexponenten:
- Primfaktorzerlegung von 125: 5 x 5 x 5 = 5^3 (sprich: 5 hoch 3)
- Primfaktorzerlegung von 724: 2 x 2 x 181 = 2^2 x 181^1 (sprich: 2 hoch mal 181 hoch 1)
- Primfaktorzerlegung von 666: 2 x 3 x 3 x 37 = 2^1 x 3^2 x 37^1 (sprich: 2 hoch1 mal 3 hoch2 mal 37 hoch 1)
Im Falls) nehmen wir die 5^3, im Fall b) die 2^2 und die 181 und im Fall c) die 3^2 und die 37. Wenn wir diese Zahlen miteinander multiplizieren, erhalten wir:
5 x 5 x 5 x 2 x 2 x 181 x 3 x 3 x 37 = 30136500
Nun können wir unsere drei Brüche gleichnamig machen und nehmen als gemeinsamen Nenner 30136500
aus 26 / 125 wird dann: 241092 / 30136500
aus 563 / 724 wird dann: 41625 / 30136500
aus 250 / 666 wird dann: 45250 / 30136500
Jetzt können wir im nächsten Schritt die gleichnamigen Brüche zusammen zählen:
Diesen Bruch kann man nicht weiter kürzen. Aber man könnte ihn auch als Dezimalzahl schreiben. Die Division von Zähler und Nenner ergibt: